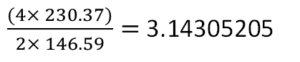Views: 17
この記事は、1年前にアップしたものですが、新たな視点を加え、再度アップします。
はじめに
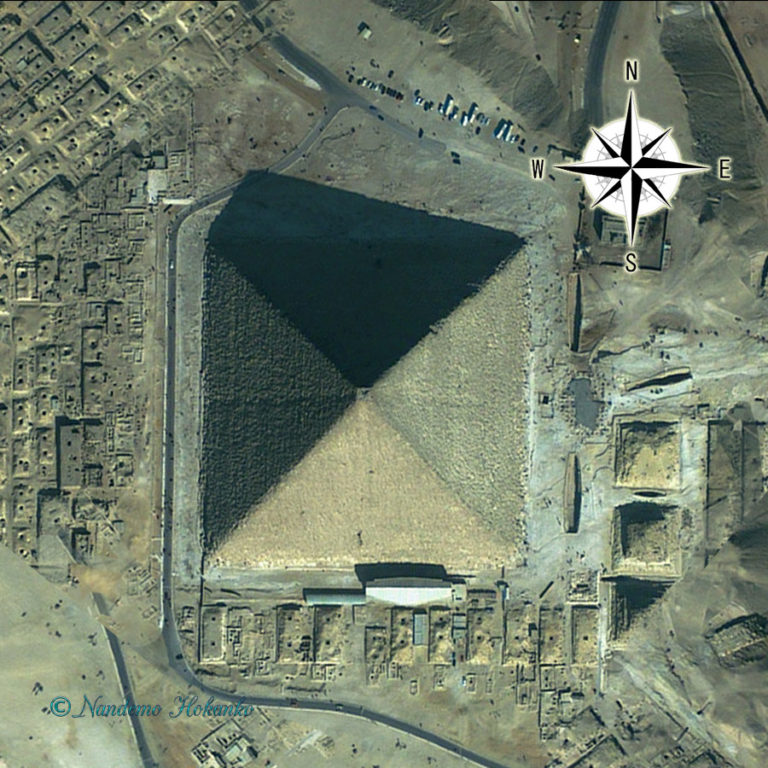
ギザ台地にそそり立つ大ピラミッド。4500年前にクフ王により建造されたとされ、その4つの面は正確に東西南北を向いています。

Source: Google Earth
なぜこれほどまでに正確なのか。古代エジプト人は、現代人の知らない高度に発達した科学技術を持っていた。
よく聞くフレーズです。でも、人の話は疑ってかかりましょう(笑)。
「未知の技術」って、あなたが知らないだけじゃないの? 高度に発達した技術って、自分の知らないことについて、そう思い込んでいるだけじゃないの?
このようなテーマに対して、テレビで有名大学を出ている連中がおバカなことばかり言って大衆をミスリードしているように感じます。
今回は、クフ王のピラミッドの造り方についてのなぞの解明です。簡単な道具だけで、正確無比に東西南北を向いたピラミッドのベースを設定する方法をご紹介します。小学生レベルの算数でできる方法です。
(建造の謎については、過去記事『世界遺産 大ピラミッド建造の謎の解明に挑む』および『クフ王のピラミッド:各層の石材の大きさに驚くべき秘密が?!』で、別の視点から紹介しています。)
大ピラミッド底面ベースの造り方
1.基礎岩盤を均し、水平にします。
水平にするには、ピラミッドのベースとなる岩盤部分をメッシュ状に細長い溝を掘り、そこに水を流し入れ、水が乗らない高い部分を削り取るという作業を繰り返します。
2.水平な基礎ができたら、次は基準線を設置します。
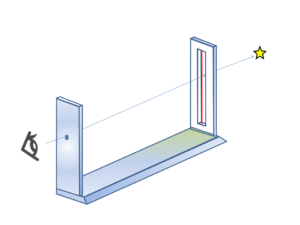
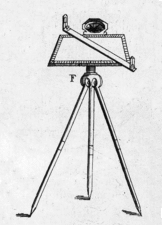
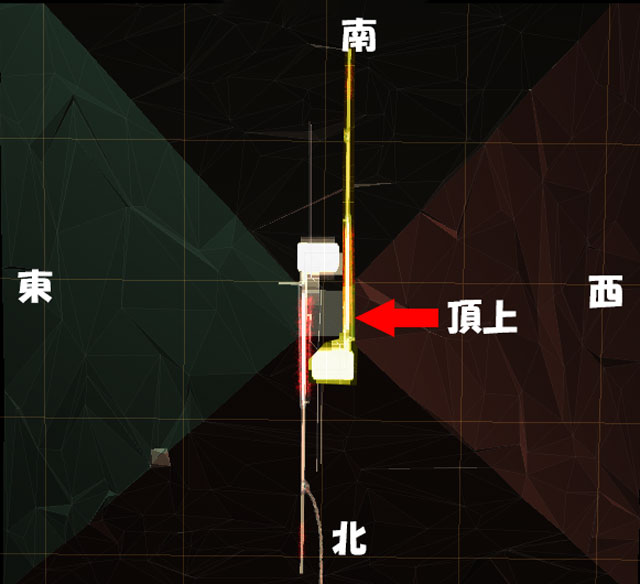
下のような簡単な構造の見通し器(アリダード、示方規)を使います。
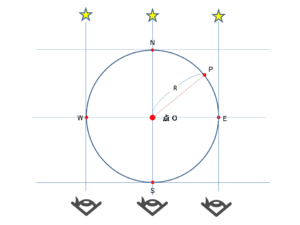
手前の小さな穴から覗き、奥に張られた赤い糸と北極星が重なるように器具を動かします。つまり、小さな穴から赤い糸越しに北極星を見通す(現代の北極星とは違う星。当時、地球の自転軸(地軸)をのばした先にある星が存在しなかった可能性もあります。その場合でも、天空の観測により天の北極の位置を知ることができるので、そこに近い周囲の星を使って補正することも可能でしょう。あまり北極星にばかりこだわると間違いの元です)。これで、真北を指し示す基準ラインができます。
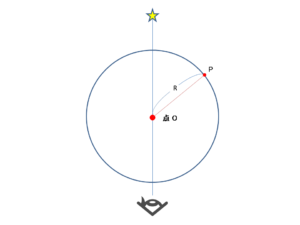
3.作業員が基盤面の中央付近に立ち、2.の見通し線上に乗る位置まで移動します。
ピッタリの位置に来たらそこを「O点」とします。これが円の中心、かつ、ピラミッドの中心になります。
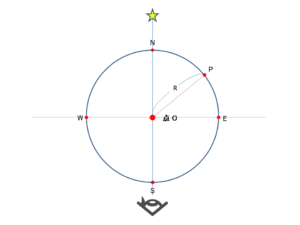
5.描いた円周上で、見通し線と交わる箇所をN点、およびS点とします。
また、O点を通り、基準線に直角な線を描き、円との交点をE点、W点とします。
どうやって、直角を正確に設定するか。これには、「3:4:5の三角形」の原理を使います。長いヒモを用意し、ある基準長さ(なんでも良い)を1とし、その長さの3倍、4倍、5倍の位置に印を付けます。そして、ヒモを引っ張り、印の位置を頂点とする三角形を作ると、直角三角形ができます。
次に、誤差をキャンセルします。
同じヒモを使い、最初に付けた印の順番とは逆の順番でヒモに印を付けます。つまり、5倍、4倍、3倍という順番で印を付けます。そして、上と同様に三角形を作り、東西方向を示す前回のラインとの誤差を確認します。前回ラインと今回のラインの平均が最も誤差を小さくできるラインになります。
上の記述では2回しか測らないように思われますが、実際にはそれぞれ、10回、あるいはそれ以上数多く測定することで誤差を小さくすることができます。
ヒモを使うため、ヒモの伸びが生ずることから必ずここで誤差が発生します。誤差をキャンセルするには、上で書いた方法が一般的でしょう。
6.次に、円周上のE点、W点を通る基準線と平行な線を引きます。
基準線を引く時と同じやり方です。星は無限遠の距離にあるので、星を見通せば平行線を簡単に引けます。
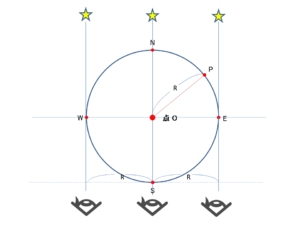
8.引いた平行線をつなげば作業終了です。
後は、検証作業。正確な正方形になっているか確認し、誤差がある場合は、誤差をキャンセルする作業を繰り返します。正方形の1辺は2Rになっている筈です。
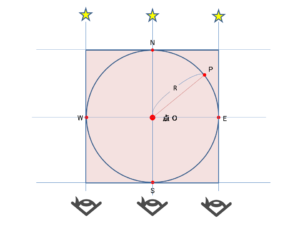
見通し器(アリダード)の大きさは、長さが1m程度必要でしょう。長いほど誤差が小さくなります。しかし、長すぎると糸が見えない。なにしろ、星が出ているのは夜なので。
これで、驚くほど正確に東西南北を向いたピラミッドのベースができます。
高度な科学知識などどこにも使っていません。
そして、当然ですが、半径Rの円に外接する正四角形なので、そこにはπ(パイ)の要素が入ることになります。πを知っていなくともこのような方法で作図するとπの要素は自ずと入り込むことになります。
計算してみたら、限りなく円周率(π)の値に近づいた。古代エジプト人はπの概念を知っていた!
これもよく見かける記述ですが、嘘っぱちなことが分かると思います。図解法で解いた値を見て、数値解法で解いた値とこれを比較し驚異的精度!と言っているようなものです。
この手の記述をする人は、権威付けするために有名な数学者、建築家が計算した結果・・・、のような書き方をしますが、それは何世紀前のことなのでしょうか。出典の学者はその後、自説を修正していないのでしょうか。
ピラミッドのサイズに見られるπ(パイ)の謎
ピラミッドの4つの底辺の和を高さの2倍で割ると円周率「π」の値に近い数字になります。
これはイギリスの数学者ジョン・テイラー(John Taylor)が発表したもので、古代エジプトで円周率の考え方が知られていたと考える根拠になっています。
さらに、テイラーは、ピラミッドの底辺と高さは、地球の円周と半径の関係に相当すると考え、「大ピラミッドは地球の寸法を記録するために建てられた」という説を最初に唱えた人でした。
確かに、円周率に非常に近い値になり、とても偶然で起きるようなことではありません。
大ピラミッドの底辺: 230.37m
高さ: 146.59m
やはり、古代エジプト人は円周率を知っていて、高度な計算により大ピラミッドを造った・・・ように見えます。
しかし、上の式をよく見ると、別の見方もできるのではないでしょうか。
「4つの底辺の和を高さの2倍で割ると円周率になる」
上で示した事例を基に考えて見ましょう。以下の記述内容は、たぶん誰も見たことがないと思います。管理人ならこう考える、というバージョンなので。
底辺の一辺は2Rです。4辺の和なので8Rになります。
高さをHとすると、8R/2H=π という関係のようです。この式を変形すると、ピラミッドの高さは、次のように表されます。
H=R/π
ところで、半径Rの円周の長さLは2πRです。(L=2πR)
これを上の式に代入するとピラミッドの高さは、H=L/2 というシンプルな式で表すことができます。
つまり、ピラミッドの高さは、半径Rの円周の長さの半分ということになります。ヒモを円周上に置き、そのヒモを半分にしたものがピラミッドの高さと言うことです。この方法を採れば円周率の計算は不要です。円周率を知らなくとも大ピラミッドを造ることができます。
管理人は、大ピラミッドの設計、施工はすべて図解法で考えるべきだと思っています。その理由は精度があまりにも高いためです。これを円周率や三角関数を用いた数値解法で解くと、必ず大きな誤差が発生します。それは有効数字の取り扱いが難しいためです。図解法ならその誤差はゼロになります。
誤差が小さい、ということは、円周率は使っていないという証明になるのではないでしょうか。もし、円周率にこだわるとするのなら、円周率の有効桁数は小数点第何位なのか明示する必要があります。
現代の数学者ならば、テイラーの仮説を一笑に付すでしょう。現代の数学者で大道芸人でもあるピーター・フランクルが、数学的に偶然の一致であるにもかかわらず、あたかも意味があるかのごとく説明する偽理論をテレビでやんわりと批判していました。
ジョン・テイラーが著書『大ピラミッド――それはなぜ建てられたか? だれが建てたか?』を発表したのは1859年のこと。今から157年も前のことです。その情報だけが一人歩きをして、現代でもそれが正しいものであるかのごとく引用している人がいます。他人の文献をコピーペするだけでなく、少しは自分で計算したらと言いたいですね。
1859年といえば、日本では、京都で和宮降嫁についての折衝が行われていた時期です。こんな昔の、現代から見ればお笑いとしか思えないような仮説を現在でも通用する仮説であるかのようにもっともらしく紹介しているサイトを見ると・・・・・ページを閉じます。
施工管理はどうやったのか
大ピラミッドは正四角錐の形をしており真正ピラミッドと呼ばれています。底盤は正確な正方形になっています。
このように規則的な形状をしているため、造るのは簡単そうに思えますが、それはサイズが小さい場合のこと。大ピラミッドのように巨大なサイズの場合、どうやって正確に石材を積み上げたらよいのか途方に暮れてしまいます。
なぜ難しいのか。それは、ピラミッド表面の傾斜角が場所によって異なるためです。
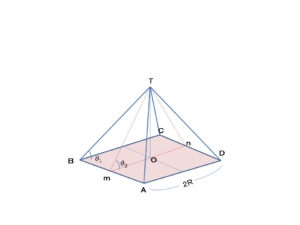
下の図を見れば分かると思います。
一般に、ピラミッドの傾斜角とは、図の角Tmn(θ2)のことを指すようです。ところで、線分TBが底面となす角θ1は、θ2とは違った角度になっています。θ1が最もきつく、θ2が最も緩い角度で、それ以外の場所ではこの2つの角度の間の角度になります。
さて、このような場合、どうやって次の段を積めばよいのでしょうか。
大ピラミッドは頂上のキャップストーンを含めて210段でできています。
下のGIFアニメをご覧下さい。全体で9段で作りました。これが大ピラミッドとするならばGIFアニメの1段が大ピラミッドの23段分に相当します。
大ピラミッドは水平に積んでいったと考えられます。その理由は簡単。外側の傾斜角をそろえるのがとても難しいから。上のGIFアニメでもきれいな傾斜角度になっていません。
サイコロのような同じ大きさの石材なら積むのは楽ですが、上で書いたように、大ピラミッドの各段の高さはかなりばらつきがあります。実はこれがくせ者。ピラミッドの傾斜角を正確に保ちながら石材を積んでいくために、石材の高さに応じて下の段よりも内側に引っ込める長さを変える必要があります。
しかも、各段の石材の高さは、同じ段であっても場所によって異なります。
ピラミッドの『面』をそろえるために、見通しを利用したと考えられます。このため、ピラミッドの各面の延長線上に見通しができる櫓(やぐら)を組んだと思います。
問題は、傾斜角の確認方法です。『面』を一直線上にそろえるのは見通しでできますが、そこに並ぶ石材の高さはまちまちです。これでは正しい傾斜角度で積めません。つまり、『面』を一直線上にそろえてはダメなのです。
ずっとこの問題を考えていたのですが、ふと、次のことに思い至りました。
大ピラミッドはなぜ八角形なのか
なぜ、大ピラミッドは上から見ると八角形なのか。
「えっ、何を言っているの? 上から見たら四角形じゃん!」
大ピラミッドを上から見ると、四角形ではなく、実は、八角形の形をしています。大ピラミッドの様々な寸法を数秘学の点から述べている論文はこのことを完全に無視していますが。
確かに、大ピラミッドはとても正確に造られた構造物です。それなのに正四角錐ではない。各辺の中央部分がピラミッドの内側に入り込んだような形をしています。
これは航空写真で見てもほとんど気がつかないほど微妙な形状の変化です。現地で大ピラミッドの前に立っても、そのような変化点があるなど全く気がつきません。
なぜ、このような形をしているのか。「特定の日に太陽の影がピラミッドの面を照らした時に影ができる。」 そのようなことを言い出す人がいます。チチェン・イッツアのピラミッド「エル・カスティージョ」と混同しているようです。「エル・カスティージョ」はピラミッドの向きがそのように設計されていますが、大ピラミッドは正確に東西南北の方向に向いています。
この八角形の謎は施工面から説明できないのでしょうか。
管理人は、施工誤差からこのようになったのではないかと考えました。
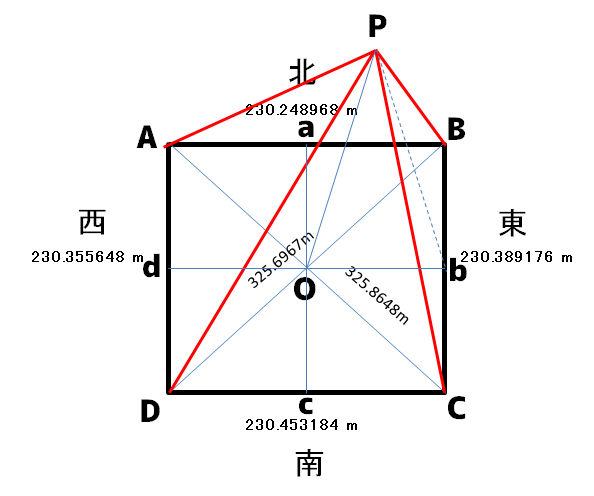
下の図をご覧下さい。少し歪な図になってしまいましたが、線分POは鉛直で、底面と直角に交わると考えて下さい。
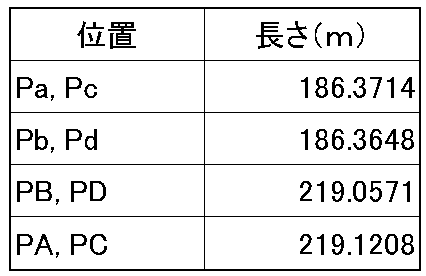
ピラミッドの斜面の長さは場所により異なります。また、底面の正方形も誤差があります。これを加味して斜面長を算出します。
斜面長は、最大で219.1208m、最小で168.3648mです。これ以外の場所の斜面長は、この値の間になります。これを上回ることも下回ることもありません。
管理人が考えたのは、施工段階で測量する場合の固定点についてです。
上で述べたように、中心点Oを基準に全ての寸法が測定されます。従って、中心点Oは施工中であってもその位置は確保されていたと考えます。つまり、O点に芯柱を立て、盛り立てが進んでも芯柱を上に伸ばし、O点の位置をキープしていた。
日中の作業が終了し、夜になると測量が始まる。底盤の測量と同じ要領でO点と各段の四隅の位置、東西南北の縁の位置を正確に決める。これにより、これらの位置はとても正確に保たれる。しかし、中間地点は若干の誤差が発生する。
石材をどうやって上まで運びあげたのか
もう一つ、八角形になっている理由として考えられるのは、石材を積み上げる過程で、荷重がかかり、内側に引っ込んでしまったということ。
各段を積み上げた時は正規な位置であったが、その後、横方向の荷重が加わり、内側に引っ込んでしまった。
そう考えることもできます。では、その時の「横方向の荷重」とは一体何だったのか。
それは、以下の図を見れば分かるのではないでしょうか。
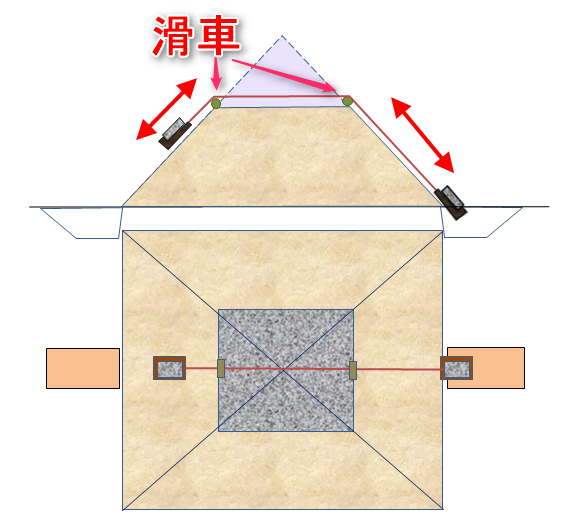
ある程度の高さまで盛り立てた後は、ピラミッドの東西南北の面を使って、『釣合重り』のように石材を持ち上げる。
図だけでは分かりにくいもので、模型を造ってみました。
ピラミッドの高さは、三分の二積んだ高さにしました。
大ピラミッドを2/3の高さまで積むとこのような形状になります。何事もやってみなければ分からない。
この『釣り合い錘』は、片方に石材を、もう片方に人が乗ります。石材の平均重量は2.5トン。これと釣り合う錘としての作業員の数は、体重60KGの作業員42名となります。実際には、摩擦などがあるので、50人くらいの作業員が乗ると動きそうです。
この装置は、エレベーターと同じで、石材を上げると同時に、作業員たちを一気に地上に降ろすという二重の効果があります。
このメカニズムが機能するためには、ロープの材質が問題になります。長大なロープを何本も使ったことでしょう。その材質は何だったのか。
管理人は、女性の毛髪だったのではないかと思います。現に、京都の東本願寺に、寺の巨大な柱を運ぶときに使った女性の毛髪と麻を編み込んだロープ(毛綱)が展示されています。太いもので長さ110cm、太さ40cm、重さ約1トンにも及ぶとか。

Photo:ネコ師
大ピラミッドのすぐ脇で太陽の船が発掘されています。このピットは、ピラミッドを造るときに使った穴を二次利用したものではないでしょうか。
ピラミッドの表面は鏡のように磨かれた化粧板石で覆われています。この化粧石盤はピラミッドの完成後、最後に貼り付けた訳ではありません。そのような施工はできません。それをやる方法がないのです。
ピラミッドの各段は化粧石を貼り付けた完成形にまで仕上げたことは間違いないでしょう。
この『釣合重り』の一方には運び上げる石材、もう一方には運び上げる石材より少し軽い石(重石)と作業員が乗ります。数人の作業員が重石として乗ることで釣り合いが崩れ、石材が上まで運び揚げられます。
この釣合重りの装置は、南北方向と東西方向の2箇所にあったのでしょう。
ピラミッドの斜面表面には化粧石盤が貼られ、表面はとてもなめらかで摩擦抵抗はとても低い。この方法で問題となるのはロープと滑車の強度くらいで、とても現実的な方法だと思います。
ところで、この方法で石材を持ち上げていくと、斜面に水平方向の偏圧がかかります。
毎日、膨大な量の石材を斜面を滑らせてリフティングするうちに、偏圧の影響で斜面が徐々にピラミッドの内側にめり込んでいく。ただし、その量はわずかなもの。石材は基本的に伸縮しないので、めり込んだのは石材同士の隙間が詰まったからでしょう。
このような仮説を提示しておきながら、自らこの仮説の問題点を指摘しておきます。釣合重りの装置を使うには、上図のように基盤面を深く掘り込んだピットが必要となります。
大ピラミッドの南面の直ぐ近くから太陽の船が発見され、現在、博物館になっています。その位置はまさにピットの位置にあたります。ピットの穴を拡大して太陽の船を収納したようにも思えます。
ところが、他の面ではこのような痕跡は見つかっていません。
大ピラミッドを訪れた観光客は、通常、北側の駐車場に車を止め、北側にある入口からピラミッドの中に入ります。しかし、北側にはピットの痕跡はなく、岩盤がむき出しのように見えます。
ピラミッドの南側から最初の太陽の船が見つかったのは1954年のこと。1987年頃に、二つ目の太陽の船が最初に見つかった船の少し西側から発見されています。このように、ピラミッドの足下はまだまだ調査されていないことが分かります。もし、ピットの跡が確認されれば、この仮説が有力になると思うのですが。
誰も指摘しない内部空間の配置
管理人が気になっているのが、『王の間』と呼ばれる部屋を支える壁の基礎部分です。
『王の間』の上部には『重量軽減の間』と呼ばれる構造があります。しかし、その構造体の壁はすべて『王の間』の壁の直上にあります。
この構造は、『王の間』という空間を創設するために設計された、という視点のみが先行していると管理人は考えます。この構造は、王の間の天井にかかる重量を軽減する機能がありますが、軽減された荷重はすべて四面の壁で支えることになります。そして、壁の基礎部分に応力が集中します。
大ピラミッドが一枚岩のような均質な構造体なら問題ないのですが、実際には、石材の空隙にがれきを詰め込んでいる箇所もあり、大ピラミッドは立方体の石材だけでできているとは言えないようです。このため、壁面直下にかかる応力は、その下の基礎部分で分散できず、直接、下方向に作用すると考えます。
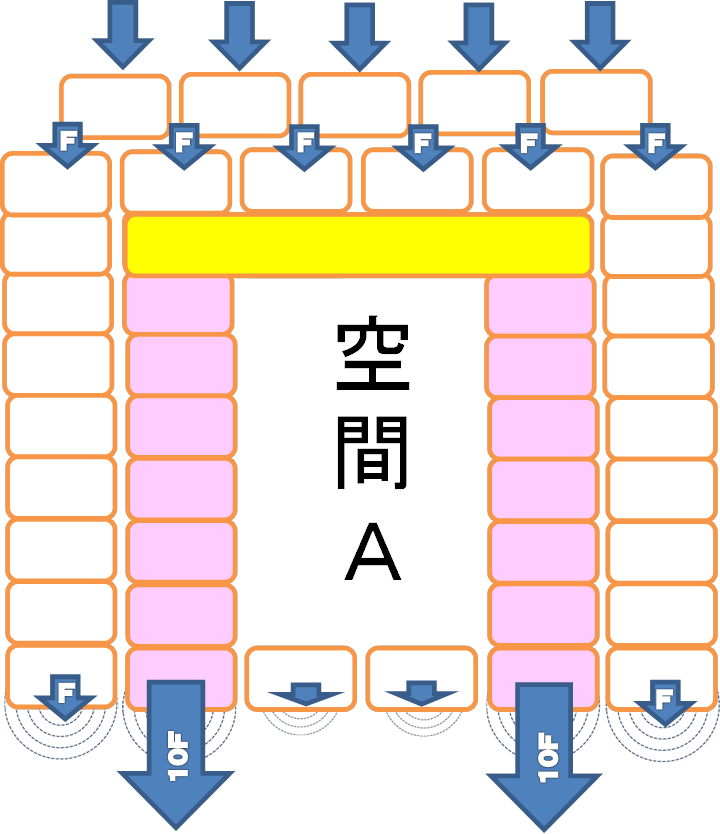
(空間Aの床面には、石材の自重しか荷重がかからないが、その脇の壁材の基礎部分には天井の梁で支えた荷重と壁の自重が集中し、周囲の石材の10倍程度の応力が集中すると考えられる。
すると、『王の間』の壁の基礎部分がどうなっているのか気になります。常識的に考えるなら、王の間の壁の基礎は、基礎岩盤から積み上げられた特殊な基礎になっていると考えられます。そうでなければ、壁の基礎部分が座屈崩壊する恐れがあります。
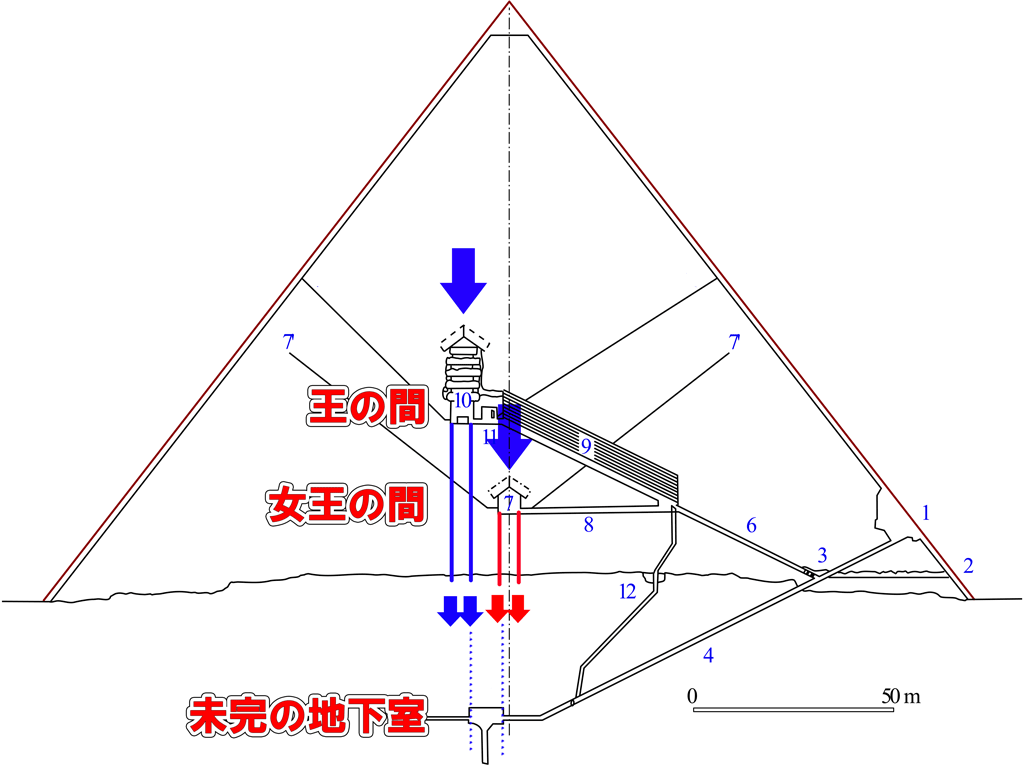
現に、『女王の間』、『未完の地下室』等の施設は、王の間の直下にはありません。壁の直下に空間ができないように位置をずらしているのが下図から分かると思います。
空間の直下に空間を造らないのではなく、『壁』の直下には造らないということです。
この構造のルールを知ると、どこに未発見の空間が存在する可能性があるかが分かります。
大ピラミッド内部で見つかった巨大空間
2016年5月1日にNHK総合で『古代遺跡透視「プロローグ 大ピラミッド永遠の謎に挑む」』が放映されました。そして、2017年11月4日、『古代文明 大ピラミッド 発見!謎の巨大空間』という番組が放映されました。
最初の番組の内容は、NHKホームページに以下のように書かれています。
その後の調査結果を伝えたのが、2017年11月放映のドキュメンタリーでした。
内容は、NHKホームページに以下のように書かれています。
日本の科学者たちが2年に及ぶ調査を行った結果、クフ王の大ピラミッド内部から、謎の巨大空間と謎の通路が発見された。ピラミッド建造から4500年、人類が探し続けてきた未知の大空間だ。内部には、一体何が残されているのか。 期待が高まっている。
ピラミッドの透視方法: 調査には「ミューオン」と呼ばれる宇宙から降り注ぐ素粒子が使われた。ミューオンはピラミッドの固い石でも通り抜ける性質を持つ。もし未知の空間があれば、その場所はより多くのミューオンが通り抜ける。この性質を利用し、今回、未知の空間を発見することに成功した。
内部へと続く謎の通路: 発見された謎の通路の幅は1~2m、高さは1~3m。ピラミッド北側斜面から内部へと伸びていることから、通路だと見られている。ピラミッドに入るには、入り口から下に向かって伸びる下降通路と、何者かが掘り進めた盗掘口があるが、それとは別にもう一つの通路があったということだ。
この空間はどこまで伸びているのか? 謎の巨大空間へと至る通路なのか? 今後の調査が待たれる。
NHK ホームページこの調査により、二つの大きな発見がありました。一つは、大回廊の上部に巨大な空間が存在すること、もう一つは、ピラミッドの入り口。大ピラミッドの正規の入り口と盗掘者が開けた入り口の二つがあるのが確認されていましたが、さらに、もう一つ、別の入り口を示す空間構造があることが分かりました。
今回見つかったこの二つの場所は、NHKのホームページで3Dで確認できます。
管理人が着目したのは、大回廊の上の巨大空間。下の動画で赤い点の集まりで示されている部分です。
これって何だろう? いや、この位置に空間なんて造ることが構造的に可能なの?
大回廊の直上に巨大空間を造ることは不可能だと、管理人は考えます。もし、この位置が少しずれていたらどうでしょう。空間を支える壁の鉛直線上に他の空間がなければ、可能かもしれません。
大ピラミッドの北斜面には内部へ入る正式な入口と盗掘者の入り口があります。
下の図をご覧ください。ピラミッドを上から見た図です。下が北になっています。
気づくのは、王の間が南に偏っていること。さらに、入り口から大回廊、王の間まで一直線ですが、ピラミッドの中心線より東側に偏った配置になっています。
これまでの検討を踏まえるならば、大ピラミッドの謎の空間の配置は、下図のようになると考えます。シンメトリーが好きな古代エジプト人が、配置をずらす理由は、ここにあります。同じシンメトリー構造のものがある。
大回廊の直上に巨大空間を造ることはできません。その空間を支える壁の荷重で大回廊の持ち送り構造の天井が崩壊します。
もし、NHKの画像が示す赤い点の集合している場所に空間を造るとすれば、大回廊と全く同じ幅の構造物になります。大回廊の壁と巨大空間の壁の位置をピッタリ一致させる。
その空間の機能は、重量軽減の間と同じなのかも知れません。でも、傾斜構造物のため、造るのはとても難しい。現実的ではないでしょう。
このため、管理人は、上図のシンメトリー構造の方がありそうな気がします。調査結果とは位置が違いますが。
ピラミッド内部の応力分布は、FEM解析をすれば分かります。誰かやっていないか調べたら、 Mohamed DarwishEmail氏が計算し、本にまとめていました。
その内容は、挙動解析で、ピラミッド全体を連続体として解析しているようです。ピラミッド内部にある空間の評価は行っておらず、管理人の関心のある王の間の基礎についての評価はできません。FEM解析はメッシュの切り方がポイントになります。誰か暇な人が解析してくれるとうれしいのですが。

The three dimensional finite element model of the great pyramid.”Variation of the Structural Dynamic Characteristics of the Great Pyramid with the Limestone Properties”
管理人は二次元でしかやったことがないので、三次元解析のやり方が分からない。どうやってメッシュを切るのだろう? 興味はあるのですが、深入りすると膨大な時間を失うことになるのでやめておきます。
玄室上部の重量軽減の間のなぞ
クフ王のピラミッドにはいくつもの謎があるのですが、今回は、クフ王の”玄室”とされる空間の上に広がる不可思議な構造について考えてみたいと思います。
一般には、「重量軽減の間」とも呼ばれているようです。
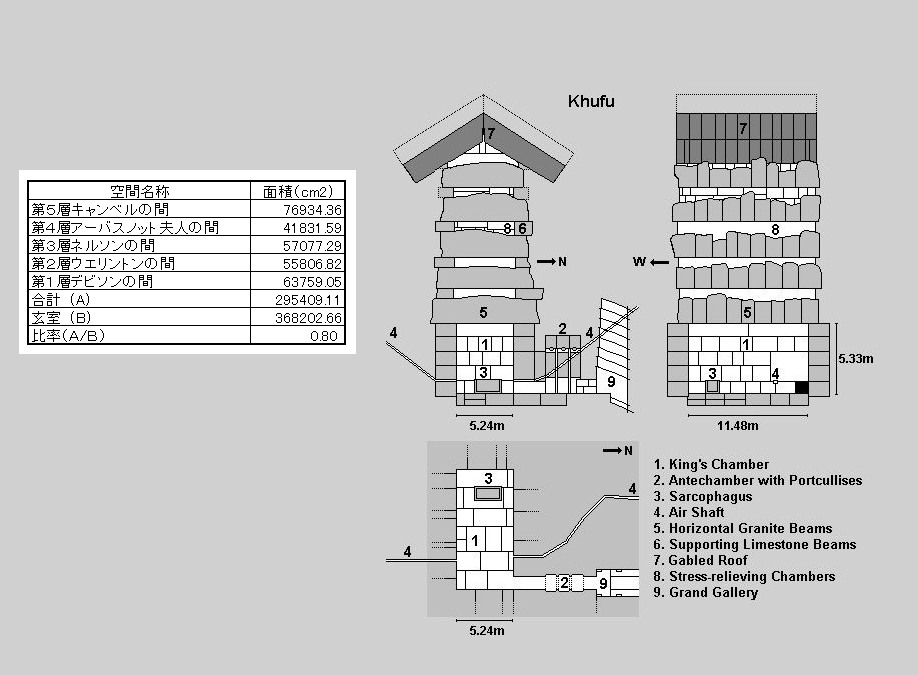
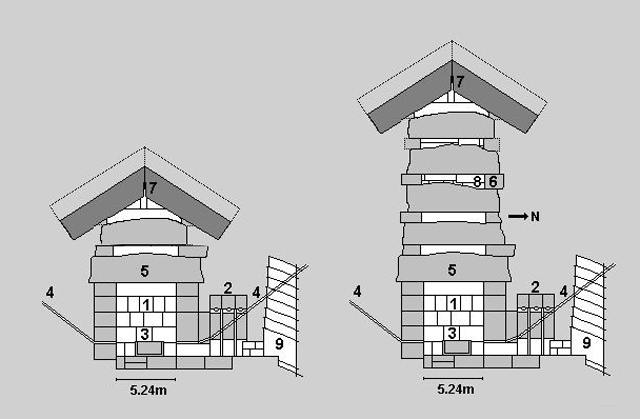
この謎の空間は全部で5層からなり、それぞれに名前が付けられています。
第1層 デビソンの間(Davidson Chamber)
第2層 ウェリントンの間(Wellington Chamber)
第3層 ネルソンの間(Nelson’s Chamber)
第4層 アーバスノット夫人の間(Lady Arbuthnot’s Chamber)
第5層 キャンベルの間(Campbell’s Chamber)
管理人の疑問は、なぜ5層なのかということです。重量を分散させるだけなら、最上部の構造だけでも良さそうに思えます。
ふと、空間の容積が重要なのではないかという考えが浮かびました。5層の空間の容積の合計が玄室の容積と一致するのではないかと。
そこで、実際に計測してみます。
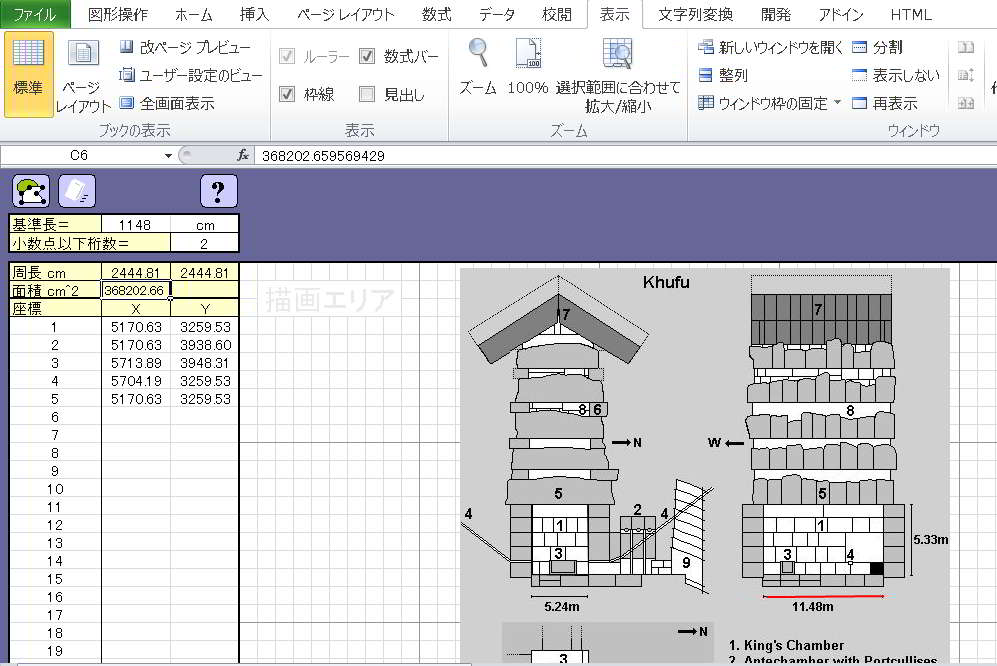
今回は、面積測定ソフト『!0_0! Excel 「長さ・面積測定」2.20b』を使って計測します。
その結果は下のようになりました。かなりアバウトな計測ですが、大まかなイメージをつかむことができます。
計測結果は、重量軽減の間の空間の合計は、玄室の約8割であることが分かりました。なお、一断面の面積から算出しているので、容積ではないのですが、概ねの傾向はこれで知ることができるでしょう。
重量軽減の間が何故5層になっているのか。それは、玄室の容積に見合う空間容積をその上部に確保したから、と言えなくもない。
もし、そうであるとしたら、なぜ?
玄室の天井、つまり、梁材にかかる荷重を軽減したいのであれば、第5層のキャンベルの間の構造で事足ります。その下の4層は不要です。
やはり、玄室と同じ容積の空間を玄室上部に設け、荷重を軽減したとしか考えられない。でも、構造的には、意味があることとは思えない。
おわりに
大ピラミッドは驚くべき構造物であることは間違いありません。しかし、現代から見れば当たり前で驚くような事柄ではないような内容を「驚くべきこと」として紹介している記事がネット上に散見されるので、この記事を書いてみました。
そもそも、ピラミッドが驚く精度で東西南北を向いており、その誤差は○○秒、などという記述をする人がいますが、それはどうやって驚くほど正確だと分かったのか、つまり、ピラミッドの基準線には何を使い、その想定基準線自体、どのくらいの誤差を持っているのか、という管理人の疑問に答える記事は皆無です。
同様に「4つの底辺の平均の長さ 230.36メートル(誤差数ミリ)」という記述もよく見掛けますが、数ミリの誤差の計算式を見てみたいものです。
基準となったであろう点は1カ所確認されているようですが、それがどこなのかという情報は見たことがない。東西南北4点の基準点が見つかったという話は聞きません。ピラミッドの前に立つと、その大きさに圧倒されます。そして、ミリ単位の誤差を測定できるような、そのための基準となるものは存在しないことも分かります。ピラミッドの四角(よすみ)から測量ピン跡でも見つかれば話は別ですが。ミリの話をするのなら、「ピン跡」です(笑)。
専門家と言われる人たちは、調査結果を公表する際に、前提条件も必ず公表します。その前提条件の意味も分からない素人が、「著名な専門家がこう言った」として、とんでもない計算をします。有効数字の意味も分からないのに驚くべき精度などと煽る記事を書く。知っていて書いているのではなく、本当に知らないのでしょうね。お気の毒様。出発点が間違っているので、この手の研究者の末路はご承知の通り悲惨な結果となります。
大ピラミッドに対する評価の視点が誤っていると感じています。本当に驚くべきことは別にあります。